如何优雅地证明二元调和平均数不大于算术平均数
证明命题
∀a,b∈R+,a1+b12≤2a+b
证明
构造函数
f(x)=x1(x∈R+)
在其上图像任取两点 A(a,a1),B(b,b1),不妨设 a≤b,如图
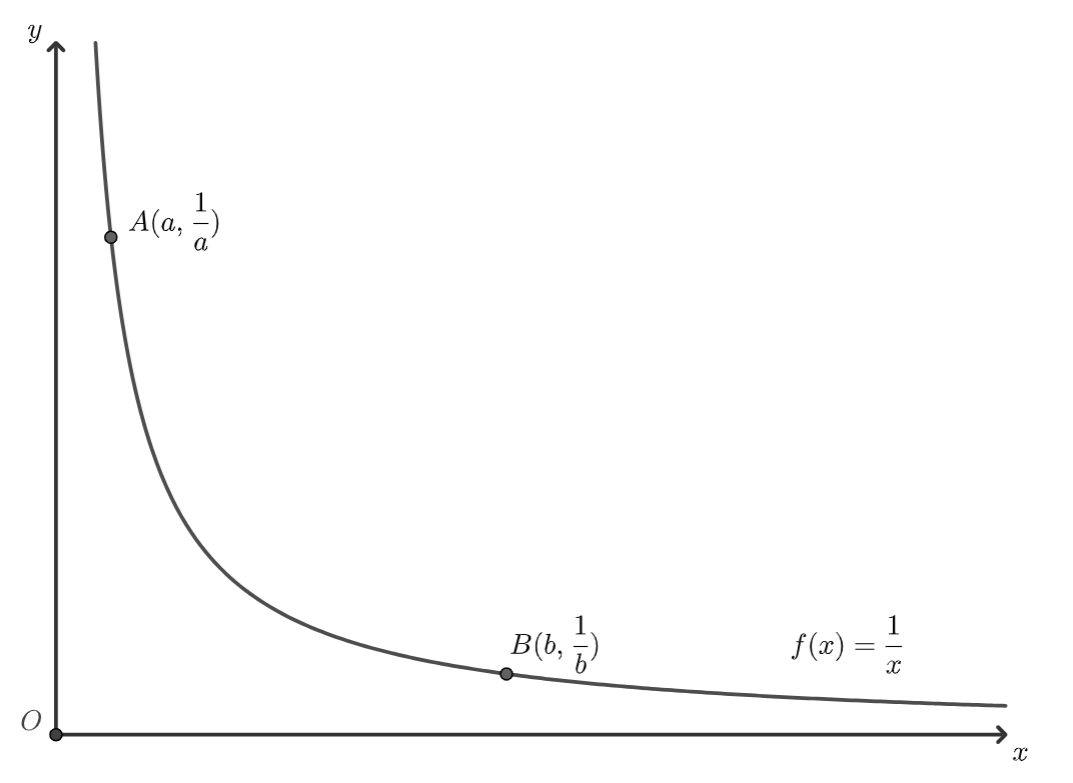
连接 A,B 并取中点 P(2a+b,2a1+b1)

过 P 作x轴平行线交 f(x) 图像于点 Q(a1+b12,2a1+b1)

观察可知,f(x) 为凸函数
严谨来说,求 f(x) 的二阶导数
dx2d2f(x)=x32>0
因此显然 xQ≤xP(其中当 A,B 重合时即 a=b,P,Q 重合,xQ=xP)
即
a1+b12≤2a+b,其中 a,b∈R+
Q.E.D





